Question

7.26. Ben leaves his house at 7 a.m. and bikes at a constant speed of 15 miles per hour due east. Alisha lives 100 miles due east of Ben, leaves her house at 8 a.m., and bikes at a constant speed of 10 miles per hour due west. At what time do they meet?

Answer 1

They will meet around 11:00am-11:40am

Step-by-step explanation:

Time and consistency are key if Ben were to bike at 20 miles per hour that would change the time and be a couple minutes early maybe around 11:30am

That’s all I have (I’m not that good at math)

Answer 2

Ben and Alisha will meet at 11:40 a.m.

Step-by-step explanation:

Given: The time at which Ben leaves his house is 7a.m. and the constant speed at which he biked due east is 15mi/hr.

The time at which Alisha leaves her house is 8a.m. and the constant speed at which she biked due west is 10mi/hr.

The distance at which Alisha lives due east of Ben is
`$100 \mathrm{mi}$`.

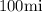To find: The time at which they meet.

a. Analyze the given data.

b. Define a variable.

c. Form an equation.

d. Solve for the unknown variable.

e. Use addition, subtraction, multiplication, or division properties.

f. Find the required time.

Step 1 of 5

Let t represent the time (in hours) from 12a.m.

We can also assume the houses as being on the number line, where Ben's house is at 0 and Alisha's house is at 100 .

Ben starts biking at 7 a.m. and he moves right (along our imaginary number line) at 15 miles per hour.

So his position at a time t is 15(t-7).

Alisha starts biking at 8a.m. and she moves left at 10 miles per hour.

So her position at a time t is 100-10(t-8).

Step 2 of 5

Ben and Alisha will meet when their positions are equal. Thus equating both the equations, we get

15(t-7)=100-10(t-8)

Using the distributive property,

15t-105=100-10t+80

Step 3 of 5

By the addition and subtraction properties,

We get,

`$$\begin{gathered}15 t+10 t=80+105 \\\Rightarrow 25 t=285\end{gathered}$$`

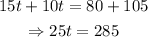
Step 4 of 5

By the multiplication and division properties,

`$$\begin{aligned}t &=(285)/(25) \\\Rightarrow t &=11.4 \mathrm{~h}\end{aligned}$$`

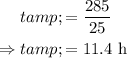
Step 5 of 5

Converting the decimal into minutes,

`$0.4 * 60=24.0 \mathrm{~min}$`

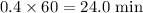
Thus the required time is 11:24a.m.