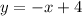Question

What is the equation of the line described below written in slope-intercept form?

the line passing through point (2, 2) and perpendicular to the line whose equation is y = x

y = x - 4
y = x + 4
y = -x + 4

Answer 1

y= -x + 4
since it is perpendicular the slope is turned the opposite direction and if you graph it out, it passes through the y-axis at (0,4) so the y-int is 4.

Answer 2

The equation is
`y=-x+4`

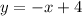
Explanation:

We know that the line must pass through the point (2,2) so it must verify the equation ⇒

a) y = x - 4

b) y = x + 4

c) y = -x + 4

If we replace the point (2,2) in the equation a)

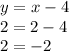`y=x-4\\2=2-4\\2=-2` that it is absurd. Therefore the point (2,2) does not belong to the line a)

If we replace the point (2,2) in the equation b)

`y=x+4\\2=2+4\\2=6` therefore the point (2,2) does not belong to the line b)

Finally,

`y=-x+4\\2=-2+4\\2=2` therefore the point (2,2) belongs to the line
`y=-x+4`

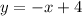
given a line

`y=ax+b`

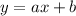
Where ''a'' is the slope. If we want to obtain a line which is perpendicular to this, we need to multiply by -1 the slope and reverse it ⇒

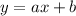`y=ax+b` is perpendicular to the line
`y=(-(1)/(a))x+b`

Now, given the line y = x the slope is ''1'' ⇒ Any line with a slope of ''-1'' will be perpendicular

The slope of the line c) y = -x +4 is -1 ⇒ y = -x +4 is perpendicular to y = x

The correct answer is
`y=-x+4`