Answer:
Hence, 0.00000103 can be expressed as
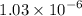 .
.
Explanation:
- Given 0.00000103
- Move the decimal point so that the factor is greater than or equal to 1 but less than 10 .
- Then count n and write no. as a product with a power of 10 .
Step 1 of 1
Consider 0.00000103,
1.03
Decimal has moved 6 places to right.
The power will be negative as the original no. is less than 1 .
