Question

If the area of a square has increased by a factor of 16, by how much has each side increased?

Answer 1

Answer: 4 times

Step-by-step explanation: If the area of a square has increased by a factor of 16,

Let us consider, the area of an old square is A and its side is
`x`.

Now, the area of a new square is 16 A and its side is
`y`

Now, we take a ratio of area of the old and new square

`(A)/(16A) = (x^(2))/(y^(2))`

`(1)/(4) = (x)/(y)`

`y = 4 x`

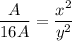
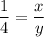
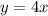
So, we can say that the sides of new square is 4 times of the sides of old square.