Question

Given quadrilateral ABCD, with vertices A (b,2c), B (4b,3c), C (5b,c), and D (2b,0), and without knowing anything about the relationship between b and c, classify the quadrilateral as precisely as possible.

A) The quadrilateral is a rectangle
B) The quadrilateral is a parallelogram
C) A quadrilateral is a trapezoid
D) The quadrilateral is a rhombus

Answer 1

Answer:The quadrilateral is a parallelogram

Answer 2

B) The quadrilateral is a parallelogram

Explanation:

WE are given the coordinates of the quadrilateral ABCD

as A (b,2c), B (4b,3c), C (5b,c), and D (2b,0)

Let us find the slopes of all sides

Slope of AB =
`Slope of AB =(c)/(3b) \\BC=(2c)/(b) \\CD=(c)/(3b)\\AD=(2c)/(b)`

From the above we know that AB and CD have same slope and hence parallel

Similarly BC and AD are parallel. Since opposite sides are parallel, ABCD is a parallelogram

To check whether rectangle, let us see slope of AB x slope of BC =-1

c/3b(2c/b) not equals -1 hence not a rectangle.

If rhombus adjacent sides should be equal

AB =
`√(c^2+9b^2)`

BC=
`√(4c^2+b^2)`

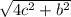
Since not equal, it is not a rhombus. ABCD is a parallelogram