Question

65. Extensions

Find the equation of the line that passes through the following points: (a, b) and (a, b +1 )

Answer 1

The equation for the line which passes through the points given as (a, b) and (a, b+1), is x=a, which represents a vertical line.

Explanation:

It is given that a line passes through the points whose coordinates are (a, b) and (a, b+1).

It is asked to find the linear equation which passes through the given points.

To do so, first determine the slope of the given line using the coordinates and the formula for the slope. Accordingly, proceed to find the equation of the given line.

Step 1 of 2

Determine the slope of the line.

The points through which the line passes are given as (a, b) and (a, b+1). Next, the formula for the slope is given as,

`$m=(y_(2)-y_(1))/(x_(2)-x_(1))$`

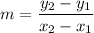
Substitute b+1&b for
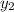`$y_(2)$` and
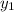`$y_(1)$` respectively, and a&a for
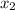`$x_(2)$` and
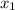`$x_(1)$` respectively in the above formula. Then simplify to get the slope as follows,

`m=(b+1-b)/(a-a)$\\ $m=(1)/(0)$`

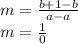
b+1. So the equation of the line cannot be found using the general point-slope form equation.

Step 2 of 2

Write the equation of the line.

So, by definition, the line that passes through the given points is a vertical line. Now, as its x- coordinate is a, so the equation of the line is given as x=a.