Question

Note: Enter your answer and show all the steps that you use to solve this problem in the space provided.

A parallelogram is shown with the diagonal drawn from the upper left vertex to the bottom right vertex.

Find the values of the variables x,y, and z in the parallelogram. The diagram is not drawn to scale.

Answer 1

x = 33 ~ Interior Angles Theorem

y = 38 ~ 33 + 109 + y = 180
142 + y = 180
__________
-142 -142
y = 38

z = 109 ~ y - Interior Angles Theorem
x - Interior Angles Theorem
33+38+z = 180
71 + z = 180
_________
-71 -71
z = 109

Answer 2

Answer: The values of he variables x, y and z are

x = 33, y = 38 and z = 109.

Step-by-step explanation: Given that in the parallelogram shown, a diagonal is drawn from the upper left vertex to the bottom right vertex.

We are to find the values of the variables x, y and z in the parallelogram.

Let us name the parallelogram as ABCD as shown in the attached figure below.

Now, since ABCD is a parallelogram, so the opposite sides will be equal and parallel. Also, the opposite angles will be equal in measure.

We have

∠ABD and ∠ACD are opposite to each other.

So,

`m\angle ABD=m\angle ACD=109^\circ\\\\\Rightarrow z^\circ=109^\circ\\\\\Rightarrow z=109.`

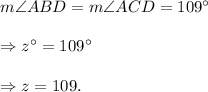
Now,

AD is parallel to BC and AC is a tranversal, so by alternate interior angles theorem, we get

`m\angle ACB=m\angle CAD\\\\\Rightarrow x^\circ=33^\circ\\\\\Rightarrow x=33.`

Also, by angle-sum-property in triangle ACD, we have

`m\angle ACD+m\angle ADC+m\angle CAD=180^\circ\\\\\Rightarrow y^\circ+109^\circ+33^\circ=180^\circ\\\\\Rightarrow y^\circ+142^\circ=180^\circ\\\\\Rightarrow y^\circ=180^\circ-142^\circ\\\\\Rightarrow y^\circ=38^\circ\\\\\Rightarrow y=38.`

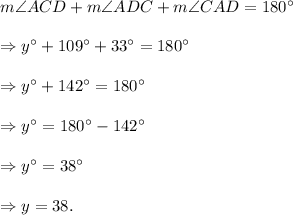
Thus, the values of he variables x, y and z are

x = 33, y = 38 and z = 109.