Question

Surface-finish defects in a small electric appliance occur at random with a mean rate of 0.3 defects per unit. find the probability that a randomly selected unit will contain at least two surface-finish defect.

Answer 1

Answer: Probability that a randomly selected unit will contain at least two surface- finish defect is 0.04.

Explanation:

Since we have given that

Mean rate defects per unit = 0.3

Since we will use "Poisson distribution":

`P(X=K)=(e^(-\lambda)\lambda^k)/(k!)`

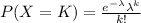
But we need to find the probability that a randomly selected unit will contain at least two surface-finish defect.

`P(X\geq 2)=1+P(X=0)+P(X=1)`

So,

`P(X=0)=(e^(-0.3)0.3^0)/(0!)=e^(-0.3)=0.74\\\\P(X=1)=(e^(-0.3)* 0.3)/(1)=0.22`

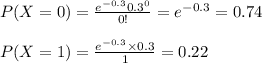
so, it becomes,

`P(X>2)=1-(0.74+0.22)=1-0.96=0.04`

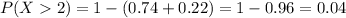
Hence, probability that a randomly selected unit will contain at least two surface- finish defect is 0.04.