Answer:
The number of people who voted is 30 people.
Explanation:
Given:
Kim was elected class president. She received 3 votes for every 2 that Amy got.
No one else ran.
However, if 8 of the people who voted for Kim had voted for Amy instead, Kim would have received only 1 vote for every 2 that Amy would have gotten
Find:
the number of people voted
Step 1 of 1
The ratio of Kim's votes to Amy's votes is 3:2, so Kim received 3x votes and Amy received 2x votes for some value of x. If 8 of the people had voted for Amy instead of Kim, then Kim would have 3x-8 votes and Amy would have 2x+8 votes. If this had happened, then Amy would have twice as many votes as Kim, so 2x+8=2(3 x-8).
Expanding the right-hand side gives 2x+8=6x-16.
Subtracting $2 x$ from both sides and adding 16 to both sides gives 24=4x, so x=6.
Since 3x+2x=5x people voted, the number of voters is
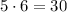 .
.