Question

Three potential employees took an aptitude test. each person took a different version of the test. the scores are reported below. vincent got a score of 83.583.5; this version has a mean of 68.268.2 and a standard deviation of 99. kaitlyn got a score of 251.2251.2; this version has a mean of 238238 and a standard deviation of 2222. reyna got a score of 8.048.04; this version has a mean of 7.27.2 and a standard deviation of 0.70.7. if the company has only one position to fill and prefers to fill it with the applicant who performed best on the aptitude test, which of the applicants should be offered the job?

Answer 1

Explanation:

To compare the performance of three potential employees, we have to convert each score into z score.

Vincent got 83.5 for a N(68.2, 99)

Z score for Vincent =
`(83.5-68.2)/(99) =0.155`

Kaitlyn got 251.2 with N(238, 22)

Z score for Kaitlyn =
`(251.2-238)/(22) =0.6`

Reyna got a score of 8.04 for N(7.27, 0.7)

Z score for Reyna =
`(8.04-7.27)/(0.7) =1.1`

Z score higher is a better option since all z scores are positive

Hence here Reyna is a good option.

Answer 2

Vincent and Reyna.

Explanation:

As z-score indicates that a data point is how many standard deviation above mean, so to find which of three applicant should be offered the job, let us find the z-score for each person using z-score formula.

`z=(x-\mu)/(\sigma)`, where,

`z`= z-score,

`x`= Random sample score,

`\mu`= Mean,

`\sigma`= Standard deviation.

`\text{z-score for Vincent}=(83.5-68.2)/(9)`

`\text{z-score for Vincent}=(15.3)/(9)`

`\text{z-score for Vincent}=1.7`

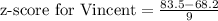
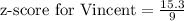
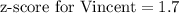
Therefore, Vincent's score on aptitude test is 1.7 standard deviation above mean.

`\text{z-score for Kaitlyn}=(251.2-238)/(22)`

`\text{z-score for Kaitlyn}=(13.2)/(22)`

`\text{z-score for Kaitlyn}=0.6`

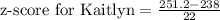
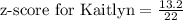
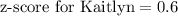
Therefore, Kaitlyn's score on aptitude test is 0.6 standard deviation above mean.

`\text{z-score for Reyna}=(8.04-7.2)/(0.7)`

`\text{z-score for Reyna}=(0.84)/(0.7)`

`\text{z-score for Reyna}=1.2`

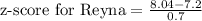
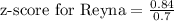
Therefore, Reyna's score on aptitude test is 1.2 standard deviation above mean.

Since Vincent and Reyna has higher z-scores, therefore, they are further above mean than Kaitlyn. Therefore, Vincent and Reyna should be offered the job.