Question

76.Real-World Applications

A cell phone company offers two plans for minutes. Plan A: $15 per month and $2 for every 300 texts. Plan B: $25 per month and $0.50 for every 100 texts. How many texts would you need to send per month for plan B to save you money?

Answer 1

For plan B to save money cell phone user need to send 6000 texts per month as
`$(x)/(y)$` expresses the average texts sent per month by cell phone user and its obtained value is 6000.

Explanation:

In the question it is given that a cell phone company offers two plans for minutes.

Plan A: $15 per month and $2 for every 300 texts.

Plan B: $25 per month and $0.50 for every 100 texts.

It is required to find that how many texts would be needed to send per month for plan B to save money. be needed to send per month for plan B to save money.

Step 1 of 6

In Plan A $15 per month and $2 for every 300 texts are costed so the cost of Plan
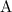`$\mathrm{A}$` is given by following equation,

`$A=15 y+(2 x)/(300)$`

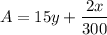
In Plan B
`$\$ 25$` per month and
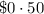`$\$ 0 \cdot 50$`for every 100 texts are costed so the cost of Plan B is given by following equation,

`$B=25 y+(0 \cdot 50 x)/(100)$`

Step 2 of 6

Now comparing the obtained equations
`$A=15 y+(2 x)/(300)$`

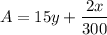
and
`$B=25 y+(0 \cdot 50 x)/(100)$`

`$15 y+(2 x)/(300)=25 y+(0 \cdot 50 x)/(100)$`

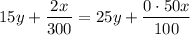
Step 3 of 6

Subtract $15 y$ from both the sides of the obtained equation
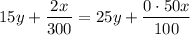`$15 y+(2 x)/(300)=25 y+(0 \cdot 50 x)/(100)$` and simplify using subtraction properties.

`$$\begin{aligned}&15 y+(2 x)/(300)-15 y=25 y-15 y+(0.50 x)/(100) \\&(2 x)/(300)=10 y+(1 x)/(200)\end{aligned}$$`

Step 4 of 6

Subtract
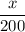`$(x)/(200)$` from both the sides of the obtained equation
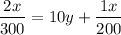`$(2 x)/(300)=10 y+(1 x)/(200)$` and simplify using subtraction properties.

`$$\begin{aligned}&(2 x)/(300)-(x)/(200)=10 y+(1 x)/(200)-(x)/(200) \\&(x)/(600)=10 y\end{aligned}$$`

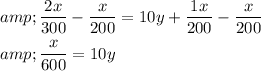
Step 5 of 6

Multiply both the sides of the obtained equation
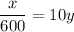`$(x)/(600)=10 y$` by 600 and simplify using multiplication properties.

`$$\begin{aligned}&(x)/(600) .600=10 y .600 \\&x=6000 y\end{aligned}$$`

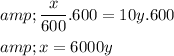
Step 6 of 6

Divide both the sides of the obtained equation x=6000 by y and simplify using division properties. As
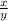`(x)/(y)` expresses the average texts sent per month by cell phone user. So, for plan B to save money cell phone user need to send 6000 texts per month.

`$$\begin{aligned}&(x)/(y)=(6000 y)/(y) \\&(x)/(y)=6000\end{aligned}$$`