Question

7.29. hose fills a swimming pool at a rate of 0.5 gallons per second. If the pool's capacity is 9,000 gallons, then how many hours does it take for the hose to completely fill an empty pool?

Answer 1

It takes the hose 300 hours to fill the pool

Explanation:

The hose can fill the pool at a rate of 0.5 gallons per second, which means that it can fill the pool at a rate of 1 gallon per 2 seconds. It needs to fill 9000 gallons of water, so assuming the ratio remains 1:2, it takes the hose 18000 (9000*2) seconds to fill the pool completely.

However, it is important to note that we have to answer in terms of hours. There are 60 seconds in an hour, so 18000 seconds is equal to 300 hours (18000/60).

Answer 2

If the pool's capacity is 9,000 gallons the number of hours it takes for the hose to completely fill an empty pool is 5 hours.

Explanation:

Given:

A hose fills a swimming pool at a rate of 0.5 gallons per second.

If the pool's capacity is 9,000 gallons, we have to find the number of hours it would take for the hose to completely fill an empty pool.

Step 1 of 1

Do a basic conversion problem:

time in seconds
`$=9000$ gallons $\cdot \frac{1 \text { seconds }}{0.5 \text { gallons }}$`

`$$\begin{aligned}&=(9000)/(0.5) \text { seconds } \\&=18000 \text { seconds }\end{aligned}$$`

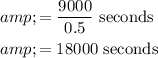
We can also convert seconds to hours using conversion factors. This gives

`$$\begin{aligned}18000 \text { seconds } &=(18000 \text { seconds }) \cdot \frac{1 \text { minute }}{60 \text { seconds }} \cdot \frac{1 \text { hour }}{60 \text { minutes }} \\&=(18000)/(60 \cdot 60) \text { hours } \\&=5 \text { hours }\end{aligned}$$`