Answer:
The required linear equation satisfying the given conditions f(-5)=-4 and f(5)=2 is
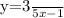
Explanation:
It is given that f(-5)=-4 and f(5)=2. It is required to find out a linear equation satisfying the conditions f(-5)=-4 and f(5)=2. To find it out, first, represent the given conditions in the form of points and then find the slope of a line passing through these two given points. Then consider one of the points to give the linear equation of the line in the form
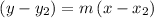
Step 1 of 4
Observe, f(-5)=-4 gives the point (5,-4)
And f(5)=2 gives the point (5,2)
This means that the function f(x) satisfies the points (-5,-4) and (5,2).
Step 2 of 4
Now find out the slope of a line passing through the points (-5,-4) and (5,2).
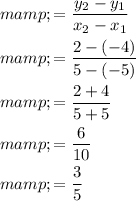
Step 3 of 4
Now use the slope
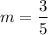 and use one of the two given points and write the equation in point-slope form:
and use one of the two given points and write the equation in point-slope form:
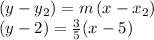
Distribute
 ,
,
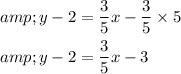
Step 4 of 4
This linear function can be written in the slope-intercept form by adding 2 on both sides,
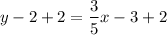
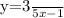
So, this is the required linear equation.