Question

7.33. Tom can paint Mr. Thatcher's fence in 6 hours, while Huck can paint Mr. Thatcher's fence in 5 hours. If they work together, then how long will it take them to paint the fence?

Answer 1

It takes them 30/11 hours to paint them together.

Explanation:

This is known as a work problem (rate * time = work). We are given the individual times for Tom and Huck (6 hours and 5 hours respectively). However, we are not given the rates at which they can paint the fence. Since we know that the total work that they both do individually is 1 (there is 1 job to do), we can calculate the rates at which Tom and Huck paint the fence on their own:

`Tom: R_(T)*6=1\\Huck: R_(H)*5=1`

We can isolate R{t} and R{h} to find the rates at which Tom and Huck work:

`Tom: R_(T)=(1)/(6)\\Huck: R_(H)=(1)/(5)`

Now, we can calculate the time it takes for Tom and Huck to work together using the same formula (the combined rate is just the sum of Tom and Huck's individual rates):

`((1)/(6) +(1)/(5))*T=1\\\\T*(11/30)=1 , T = 30/11`

Therefore, the time it takes them to paint the fence together is 30/11 Hours

Answer 2

The number of hours it will take them to paint the fence is 2.7 hours.

Explanation:

Given:

Tom can paint Mr. Thatcher's fence in 6 hours, while Huck can paint Mr. Thatcher's fence in 5 hours.

Find:

the number of hours it will take them to paint the fence

Step 1 of 1

Determine their work rates, and then add them.

In particular, Tom can paint
`$(1)/(6)$` of a fence per hour, and Huck can paint
`$(1)/(5)$` of a fence per hour.

So, together they can paint
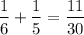`$(1)/(6)+(1)/(5)=(11)/(30)$` of a fence per hour. Therefore, the time to paint the whole fence is
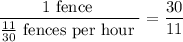`$\frac{1 \text { fence }}{(11)/(30) \text { fences per hour }}=(30)/(11)$` hours

`$=2 (8)/(11) \text { hours, }$$` or a little over 2.7 hours.