Question

66. Extensions

Find the equation of the line that passes through the following points: (2a, b) and (a, b + 1)

Answer 1

The equation of the line that passes through the points (2a, b) and (a, b+1) is
`$y=-(1)/(a) x+2+b$`.

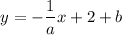Explanation:

The given points are (2a, b) and (a, b+1).

It is required to find the equation of the line that passes through the points. the slope-intercept form.

Step 1 of 4

Using the given two points, to find the slope.

Given points are (2a, b) and (a, b+1).

Substitute
`$x_(1)`=2a,

`$$\begin{aligned}&y_(1)=b \\&x_(2)=a \text { and } \\&y_(2)=b+1\end{aligned}$$`

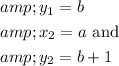
into the formula,
`$m=(y_(2)-y_(1))/(x_(2)-x_(1))$`

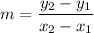
Step 2 of 4

Simplify
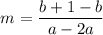`$m=(b+1-b)/(a-2 a)$`, further

`$$\begin{aligned}m &=(b+1-b)/(a-2 a) \\m &=-(1)/(a)\end{aligned}$$`

As a result, the slope is
`$m=-(1)/(a)$`.

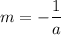Step 3 of 4

Use the slope
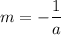`$m=-(1)/(a)$` and the coordinates of one of the points (2a, b) into the point-slope form,
`$y-y_(1)=m\left(x-x_(1)\right)$`.

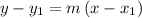Substitute
`$m=-(1)/(a)$`,

`x_(1)=2 a$ and$y_(1)=b$`

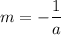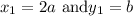
into the formula,
`$y-y_(1)=m\left(x-x_(1)\right)$`

`$y-b=-(1)/(a)(x-2 a)$`

`$y-b=-(1)/(a) x+2$$`

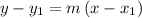
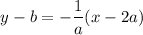
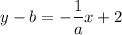
Step 4 of 4

Rewrite the above equation as a slope-intercept equation. So, from the above term
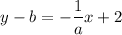`$y-b=-(1)/(a) x+2$`, Add b on each side.

`$$\begin{aligned}&y-b=-(1)/(a) x+2 \\&y=-(1)/(a) x+2+b\end{aligned}$$`

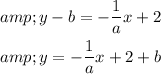
Therefore, the equation of the line that passes through the points is
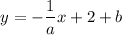`$y=-(1)/(a) x+2+b$`.