a. By the FTC,
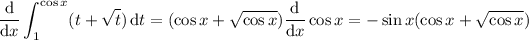
b. We can either evaluate the integral directly, or take the integral of the previous result. With the first method, we get
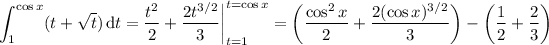
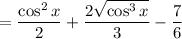
c. The derivative of the previous result is
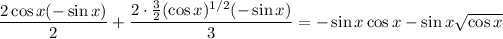
which is the same as the answer given in part (a), so ...
d. ... yes