Answer:
Point-slope form of equation given as
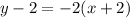 .
.
Slope-intercept form of equation is given as
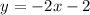 .
.
Explanation:
In the question, it is given that the slope of a line is -2 and it passes from (-2,2).
It is asked to write the point-slope form of the equation and rewrite it as slope-intercept form.
To do so, first find the values which are given in the question and put it in the formula of point-slope form. Simplify the equation to rewrite as slope-intercept form.
Step 1 of 2
Passing point of the line is (-2,2).
Hence,
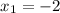 and
and
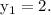
Also, the slope of the line is -2.
Hence, m=-2
Substitute the above values in point-slope form of equation given by
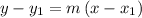
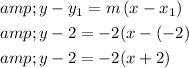
Hence, point-slope form of equation given as y-2=-2(x+2).
Step 2 of 2
Solve y-2=-2(x+2) to write it as slope-intercept form given by y=mx+c.
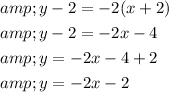
Hence, slope-intercept form of equation is given as y=-2x-2.