Question

CALCULUS EXPERT WANTED (ignore the stuff I was writing)

Edit: just found out there was a point system on this app lol

Answer 1

Given how complicated the derivative,

`f'(x)=(\cos(1-x^2))/(x^2+\sqrt x)`

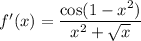
looks, integrating it to find
`f(x)` seems futile, and actually not what needs to be done. You're asked to approximate
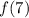`f(7)` using a given point and the value of the derivative at any point. To do that, you can use a linear approximation.

`f(7)\approx f(2)+f'(2)(7-2)`

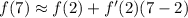
which comes from exploiting the mean value theorem (solve for
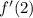`f'(2)` above to see how)

Then

`f(7)\approx8+(5\cos(1-2^2))/(2^2+\sqrt2)\approx7.086`

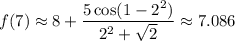
The closest answer would be B. The reason the listed answer is so far off is because 7 is not so close to 2.