Question

37. For the following exercises, given each set of information, find a linear equation satisfying the conditions, if possible.

37. x-intercept at (-5, 0) and y-intercept at (0, 4)

Answer 1

The linear equation for the line with an x-intercept at (-5,0) and y-intercept at (0,4) is found as
`$y=(4)/(5) x+4$`.

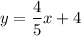Explanation:

A condition is given that a line has an x- intercept at (-5,0) and y- intercept at (0,4).

It is asked to find a linear equation satisfying the given condition.

To do so, first determine the slope of the line using coordinates of the given intercepts. Then write the equation in the slope-intercept form using the slope and the y- intercept.

Step 1 of 2

Determine the slope of the line.

The points of the intercepts of the line are given as (-5,0) and (0,4). Next, the formula for the slope is given as,
`m=(y_(2)-y_(1))/(x_(2)-x_(1))$`

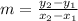
Substitute 4&0 for
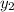`$y_(2)$` and
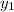`$y_(1)$`respectively, and 0&-5 for
`$x_(2)$` and
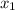`$x_(1)$` respectively in the above formula. Then simplify to get the slope as follows,

`$$\begin{aligned}m &=(4-0)/(0-(-5)) \\m &=(4)/(5)\end{aligned}$$`

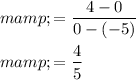
Step 2 of 2

Write the equation in the slope-intercept form.

The slope-intercept form of a line is given as follows,

`$$y=m x+b$$`

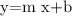
The coordinates at the y- intercept is (0,4). Now, as the y- coordinate is 4 , so b=4.

So, substitute 4 for b and
`$(4)/(5)$` for m in the equation y=mx+b, as follows,

`$y=(4)/(5) x+4$$`

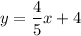
This is the required linear equation.