Answer:
The inverse of the given function is
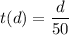 . The time taken to travel 180 miles is 3.6 hours.
. The time taken to travel 180 miles is 3.6 hours.
Explanation:
It is given that a car travels at a constant speed of 50 miles per hour. A function for distance traveled is also given as d(t)=50t.
It is required to find the inverse of the function by expressing the time travel in terms of distance traveled and also find t(180).
To find the inverse, express time traveled in terms of distance traveled using normal algebraic methods and then substitute 180 for t and explain its results.
Step 1 of 2
The given function is d(t)=50t.
Consider d(t) as d and t as t(d) and rewrite the equation.
The rewritten function is d=50 t(d)
Divide by 50 on both sides of the equation.
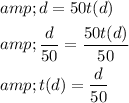
Step 2 of 2
Substitute 180 for $t$ in the simplified expression and interpret the results.
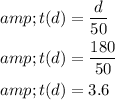
The time taken to travel 180 miles is 3.6 hours.