Answer:
The graph of h(x) is shown below.
Explanation:
The given function is
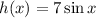
The general form of sine function is
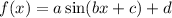
Where, a is amplitude, b is period, c is phase shift and d is vertical shift.
So, the amplitude of the given function is 7, period is 1, phase shift is 0 and vertical shift is 0.
It means the minimum value of function is -7 and maximum value is 7.
Put x=0 in the given function.

Put
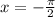 in the given function.
in the given function.
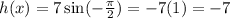
Put
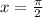 in the given function.
in the given function.
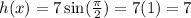
Therefore the points on the function are (0,0),
 .
.
The graph of function is shown below.