Answer:
The equation of the unknown line is
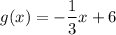 .
.
Explanation:
In the question, it is given that a line passes through (-2,-15) and (2,-3). Another line perpendicular to the first line passes through (6,4).
It is required to find the equation of the second line. of b and substitute all these values to find the equation of second line.
Step 1 of 2
Find the slope of first line.
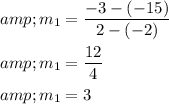
Therefore, the slope of second line is
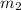 .
.
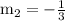
Step 2 of 2
Substitute the values of
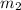 ,x and g(x) to find the b.
,x and g(x) to find the b.
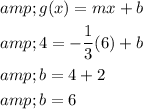
Therefore, the equation of the unknown line is
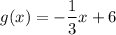 .
.
Step 1 of 2
Find the slope of first line.
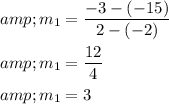
Therefore, the slope of second line is
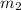 .
.
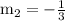
Step 2 of 2
Substitute the values of
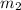 , x and g(x) to find the b.
, x and g(x) to find the b.
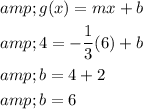
Therefore, the equation of the unknown line is
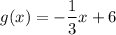 .
.