Question

4. Try It #4 Write the point-slope form of an equation of a line that passes through the points (-1,3) and (0,0). Then rewrite it in the slope-intercept form.

Answer 1

Point-slope form of equation of a line that passes from (-1,3) and (0,0) is given as y-3=-3(x+1).

Slope-intercept form of equation is given as y=-3x.

Explanation:

In the question, it is given that the line passes from (-1,3) and (0,0).

It is asked to write the point-slope form of the equation and rewrite it as slope-intercept form.

Step 1 of 2

Passing point of line is (-1,3).

Hence,
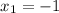`$x_(1)=-1$` and

`$$y_(1)=3 \text {. }$$`

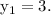
Also, Passing point of line is (0,0).

Hence,
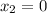`$x_(2)=0$` and

`$$y_(2)=0 \text {. }$$`

Substitute the above values to find the slope of line which is given by
`$m=(y_(2)-y_(1))/(x_(2)-x_(1))$`

`$$\begin{aligned}m &=(y_(2)-y_(1))/(x_(2)-x_(1)) \\m &=(0-3)/(0-(-1)) \\m &=(-3)/(1) \\m &=-3\end{aligned}$$`

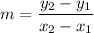
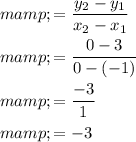
Hence, slope of the line is -3

Step 2 of 3

It is obtained that m=-3

`$y_(1)=3$`

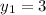
and
`$x_(1)=-1$`

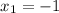
Substitute the above values in point-slope form of equation given by
`$y-y_(1)=m\left(x-x_(1)\right)$`

`$y-y_(1)=m\left(x-x_(1)\right)$\\ $y-3=-3(x-(-1)$\\ $y-3=-3(x+1)$`

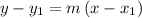
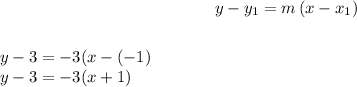
Hence, point-slope form of equation given as y-3=-3(x+1).

Step 3 of 3

Solve y-3=-3(x+1) to write it as slope-intercept form given by y=mx+c

`$y-3=-3(x+1)$\\ $y-3=-3 x-3$\\ $y=-3 x-3+3$\\ $y=-3 x$`

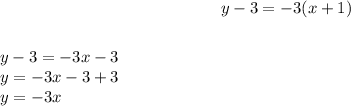
Hence, slope-intercept form of equation is given as y=-3x.