Question

Quadrilaterals part 1 introduction to quadrilaterals part 2 independent

Answer 1

1. A. Graph below

1. B. Trapezoid

2. Interior angles are 63.3°, 147.9°, 27.13° and 121.6°.

Explanation:

Ques 1: We are given that, for quadrilateral CONR,

CO is represented by the line
`y=9+2x` when
`-4\leq x\leq -3`

RN is represented by the line
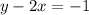`y-2x=-1` when
`-1\leq x\leq 2`

Part A). After plotting the lines, we will get the following graph.

Part B) Joining the end points, we see that, CONR is a trapezoid.

Ques 2: Since, we know,

The sum of the interior angles of a quadrilateral is 360°

So, we have,

`(3x)/(7)+(3x-42)+x+(2x-5)=360`

i.e.
`(3x)/(7)+6x-47=360`

i.e.
`(3x+42x)/(7)=360+47`

i.e.
`(45x)/(7)=407`

i.e.
`x=(407* 7)/(45)`

i.e.
`x=(2849)/(45)`

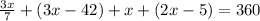
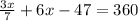
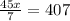
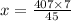
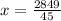
i.e. x= 63.3°

So, we have,

x= 63.3°

(3x-42)° = (3×63.3 - 42)° = (189.9-42)° = 147.9°

`(3x)/(7)=(3* 63.3)/(7)=(189.9)/(7)` = 27.13°

(2x-5)° = (2×63.3-5)° = (126.6-5)° = 121.6°

Thus, the interior angles are 63.3°, 147.9°, 27.13° and 121.6°.