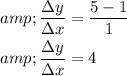Question

For the following exercises, find the average rate of change of the functions from x = 1 to x =2.

24. f(x) = 4x − 3

Answer 1

For the function
`$f(x)=4 x-3$` the average rate change from x is equal 1 to x is equal 2 is 4 .

Explanation:

A function is given f(x)=4x-3.

It is required to find the average rate change of the function from x is 1 to x is 2 . simplify.

Step 1 of 2

A function f(x)=4 x-3 is given.

Determine the function
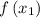`$f\left(x_(1)\right)$` by putting the value of x=1 in the given function.

`$$\begin{aligned}&f(1)=4(1)-3 \\&f(1)=1\end{aligned}$$$$f(1)=1$$`

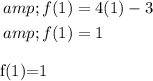
Determine the function
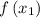`$f\left(x_(1)\right)$` by putting the value of x is 2 in the given function.

`$$\begin{aligned}&f(2)=4(2)-3 \\&f(2)=5\end{aligned}$$`

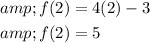
Step 2 of 2

According to the formula of average rate change of the equation
`$(\Delta y)/(\Delta x)=(f\left(x_(2)\right)-f\left(x_(2)\right))/(x_(2)-x_(1))$`

Substitute the value of
`$f\left(x_(1)\right)$` with,
`$f\left(x_(1)\right)$` with
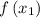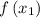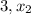`$3, x_(2)$` with 2 and
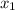`$x_(1)$` with 1 .

`$$\begin{aligned}&(\Delta y)/(\Delta x)=(5-1)/(1) \\&(\Delta y)/(\Delta x)=4\end{aligned}$$`