Answer:
See solution
Explanation:
Similar triangles have proportional corresponding sides.
1.
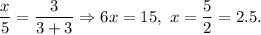
2.
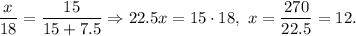
3.
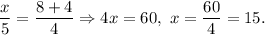
4. Angles ACB and ECD are congruent as vertical angles. Angles BAC and DEC are congruent (given), then ΔABC and ΔEDC are similar by AA theorem.
5. MN=NP=8 (given), NR=NQ=8+10=18 (given), angle N is common, then ΔNMP and ΔNQR are similar by SAS theorem.