Question

Anton's family drove 216 mi to the lake averaging 48 ​ mi/h ​ . On the return trip home they averaged 54 mi/h .

What was the total time that Anton's family spent driving to and from the lake?

8.0 h

8.5 h

9.0 h

9.5 h

Answer 1

8.5 B

Explanation:

took the test on k-12 :)

Answer 2

For this case we have that the distance that it is necessary to cross to arrive at the lake is of 216 miles.

If the family went there with an average of
`\frac {48 \ mi} {h}`

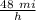
To know the time it took me to travel 216 miles, we make a rule of three:

Let "x" be the time spent going to the lake:

48 miles -------------> 1 h

216 miles -----------> x

`x = \frac {216 * 1} {48} = 4.5\ hours`

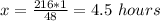
Thus, to reach the lake they had to travel 4.5 hours.

Now, back home they averaged
`\frac {54 \ mi} {h}`

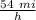
To know how much time they used back home, we make a rule of three (to return also travel 216 miles):

Let "y" be the time spent returning home:

54 miles -------------> 1 h

216 miles -----------> y

`y = \frac {216 * 1} {54} = 4\ hours`

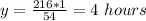
Thus, the total time is given by:

`t = 4.5 + 4\\t = 8.5`

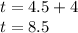
Answer:

8.5 hours

Option B