Question

Verbal
3. Can a function be its own inverse? Explain.

Answer 1

The function can have its own inverse, that is,
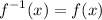`$f^(-1)(x)=f(x)$` and this type of function is called an involution. Example f(x)=6-x.

Explanation:

A statement that a function can be its own inverse is given.

It is required to explain whether a function has its own inverse. Then explain whether the given statement satisfies the condition.

Step 1 of 3

Consider a function is f(x)=6-x.

This function is a continuous function for all values of x. This function is also a linear function. So, every continuous linear function is a one-to-one function.

So, this function is one-to-one.

Step 2 of 3

Consider f(x) as y and rewrite the equation.

The equation becomes
`$y=6-x$`

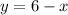
Solve the rewritten equation.

Add -6 on both sides of the equation.

`$$\begin{aligned}&y=6-x \\&y-6=6-x-6 \\&y-6=-x\end{aligned}$$`

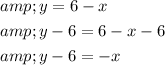
Step 3 of 3

Multiply by -1 on both sides.

`$$\begin{aligned}&y-6=-x \\&(-1)(y-6)=(-x)(-1) \\&-y+6=x \\&x=6-y\end{aligned}$$`

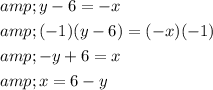
Interchange x and y in solved equation.

`$$\begin{aligned}&x=6-y \\&y=6-x\end{aligned}$$`

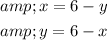
So, the inverse of the given function is
`$f^(-1)(x)=6-x$`.

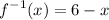The function and inverse of the function are the same, that is,
`$f^(-1)(x)=f(x)$`

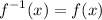
So, a function can have its own inverse. This type of function is called an involution.