Answer:
The slope of the line representing the linear function f(x) is determined as
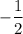 . The function f(x) is decreasing because the slope is less than zero, i.e., m<0.
. The function f(x) is decreasing because the slope is less than zero, i.e., m<0.
Explanation:
A linear function f(x) is given with two points, (2,3) and (0,4) lying on the line representing f(x).
It is asked to determine the slope of the line and state if the function is increasing or decreasing. of the value of the slope obtained.
Step 1 of 1
Determine the slope of the line.
The points as given in the question are (2,3) and (0,4). Now, the formula for the slope is given as
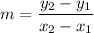
So, substitute
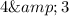 for
for
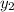 and
and
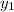 respectively, and
respectively, and
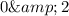 for
for
 and
and
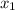 respectively in the above formula. Then simplify to get the slope as follows,
respectively in the above formula. Then simplify to get the slope as follows,

The slope of the line is obtained as
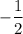 . Now, as
. Now, as
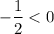 , so the function f(x) is decreasing.
, so the function f(x) is decreasing.