Answer:
The solution to the given equation is at point (1.353, 1.613). Explanation:
Given : Kim solved the equation below by graphing a system of equations.
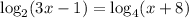
To find : What is the approximate solution to the equation?
Solution :
Let,
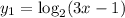
and
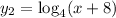
Now, we plot these two equations.
The graph of
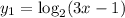 is shown with red line.
is shown with red line.
The graph of
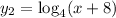 is shown with blue line.
is shown with blue line.
The solution to this system will be their intersection point.
The intersection point of these graph is (1.353, 1.613)
Refer the attached graph below.
Therefore, The solution to the given equation is at point (1.353, 1.613).