Question

32.For the following exercises, given each set of information, find a linear equation satisfying the conditions, if possible.

32. (2, 4) and (4, 10)

Answer 1

The required linear equation satisfying the given points (2,4) and (4,10) is y=3x-2

Explanation:

Two points are given in question, (2,4) and (4,10).

It is required to find out a linear equation satisfying the points (2,4) and (4,10).

To find it out, find the slope of a line passing through these two given points. Then consider one of the points to give the linear equation of the line in the

`$$\left(y-y_(2)\right)=m\left(x-x_(2)\right)$$`

Step 1 of 3

The slope of a line passing through the points (2,4) and (4,10) is given by

`$$\begin{aligned}m &=(y_(2)-y_(1))/(x_(2)-x_(1)) \\m &=(10-4)/(4-2) \\m &=(6)/(2) \\m &=3\end{aligned}$$`

Step 2 of 3

Now use the slope m=3 and use one of the two given points and write the equation in point-slope form:

`$$\left(y-y_(2)\right)=m\left(x-x_(2)\right)$$\\ $$(y-4)=3(x-2)$$`

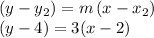
Distribute 3 ,

`$$\begin{aligned}&y-4=3 x-3 * 2 \\&y-4=3 x-6\end{aligned}$$`

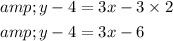
Step 3 of 3

This linear function can be written in the slope-intercept form by adding 4 on both sides,

`$$\begin{aligned}&y-4+4=3 x-6+4 \\&y=3 x-2\end{aligned}$$`

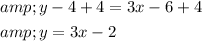
So, this is the required linear equation.