Answer:
The solution to the inequality
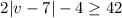 in interval notation is given by
in interval notation is given by
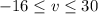 .
.
Explanation:
An absolute value inequality
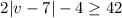 is given.
is given.
It is required to solve the inequality and write the solution in interval form.
To write the solution, first solve the given absolute value inequality algebraically and then write it in interval notation.
Step 1 of 4
The given absolute value inequality is
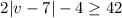 .
.
Add on both 4 sides,

Step 2 of 4
Divide by 2 on both sides,
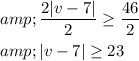
The inequality can be written as
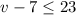 and
and

Step 3 of 4
First solve the inequality,
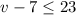 .
.
Add 7 on both sides,
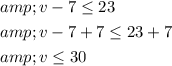
Step 4 of 4
Solve the inequality
 .
.
Add 7 on both sides,
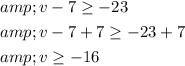
The solution of the inequality in interval notation is given by
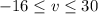 .
.