Answer:
Two options:
5,6, and 7
-1,0,and 1
Explanation:
Three consecutive natural numbers can be represented as n, n+1, and n+2.
The product of the smaller two would be n(n+1). The less than 5 times the larger is 5(n+2)-5.
Set them equal and solve by factoring:
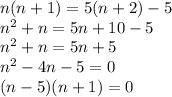
Set each factor equal to 0.
n-5==0 so n=5.
n+1=0 so n=-1.
This means the 3 consecutive numbers would be 5,6, and 7
OR
-1, 0 or 1.