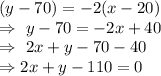Answer:
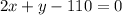
Explanation:
Given: A line is drawn through (twenty, seventy) and (twenty-five, sixty).
The points through which line is passing are (20,70) and (25,60)
The slope of the line=
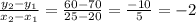
The equation of line with slope m and passing through point
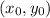 is
is
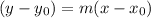
Therefore, the equation of the trend line with slope -2 and point (20,70) will be