Question

A rope is tied to the bottom of a hot air balloon as shown. The altitude of the balloon is 50 feet and the rope is 75 feet long.What is the angle that the rope makes with the ground? Round the angle to the nearest angle.

Answer 1

The angle that the rope makes with the ground is 41.8°.

Explanation:

Given : The altitude of the balloon is 50 feet and the rope is 75 feet long.

To find : What is the angle that the rope makes with the ground?

Solution :

First we refer the image attached below.

Altitude of the balloon is the opposite side AB= 50 feet

Length of the rope is the hypotenuse side AC= 75 feet

Using the trigonometric ratios,

`\sin \theta = \frac{\text{Opposite side}}{\text{Hypotenuse side}}`

Substitute the values,

`\sin \theta = (50)/(75)`

`\sin \theta =(2)/(3)`

`\theta = \sin^(-1) ((2)/(3))`

`\theta =41.8^\circ`

Therefore, the angle that the rope makes with the ground is 41.8°.

Answer 2

As per the statement

The altitude of the balloon is 50 feet and the rope is 75 feet long.

⇒ Altitude of the balloon = 50 feet.

And length of the rope = 75 feet.

We have to find the angle that rope makes with ground,

Using Sine ratio:

`\sin \theta = \frac{\text{Opposite side}}{\text{Hypotenuse side}}`

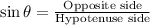
You can see the diagram as shown below.

Here,

Opposite side = Altitude of the balloon = 50 feet.

Hypotenuse side = length of the rope = 75 feet.

Substitute the given values we have;

`\sin \theta = (50)/(75) =(2)/(3)`

⇒
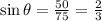
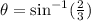`\theta = \sin^(-1) ((2)/(3))` = 41.8°

Therefore, the angle that the rope makes with the ground is, 41.8 degree