Question

What are the coordinates of the intersection of the diagonals of parallelogram LMNO, with vertices L(0,-3), M(-2,1), N(1,5), O(3,1)?

Answer 1

ANSWER


`\boxed {( (1)/(2) , 1)}`

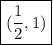
Step-by-step explanation

The given parallelogram has vertices,

L(0,-3), M(-2,1), N(1,5), O(3,1).

The diagonals of the parallelogram bisect each other.

From the diagram, we can see that, the diagonals have coordinates L(0,-3),N(1,5)

and

M(-2,1),O(3,1).

The midpoint of any of the diagonals will give us the coordinates of intersection of the diagonals.

Recall the midpoint formula,


`((x_1+x_2)/(2), (y_2+y_1)/(2))`

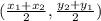
Using L(0,-3),N(1,5) gives,


`((0+1)/(2), ( - 3+5)/(2))`


`((1)/(2), ( 2)/(2))`


`((1)/(2), 1)`

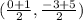
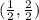
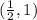
Or we could have also used,M(-2,1),O(3,1) to get,


`((-2+3)/(2), ( 1+1)/(2))`


`(( 1)/(2), ( 2)/(2))`


`(( 1)/(2), 1)`

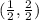
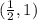
The correct answer is C