Question

A hardware store orders at most $2,500 worth of concrete and sand. The store needs to make a profit of at least $2,750 on the order. The possible combinations of concrete and sand for this order are given by this system of inequalities, where c = pounds of concrete and s = pounds of sand: 6c + 2s ≤ 2,500 4.50c + 3s ≥ 2,750 Which graph's shaded region represents the possible combinations of concrete and sand for this order?

Answer 1

top left

Explanation:

i did it

Answer 2

Answer: The below graph's shaded region represents the possible combinations of concrete and sand for this order

Explanation:

Here, the system of inequality that represents the given situation is,

6c + 2s ≤ 2,500 --------(1)

4.50c + 3s ≥ 2,750 -------(2)

Where c = pounds of concrete,

s = pounds of sand

Now, The related equation of the above inequalities are,

6c + 2s = 2500

4.50c + 3s = 2750

By solving the above equations,

We get,
`c =222.\bar{2}`,
`s = 583.\bar{3}`

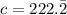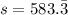
Thus, the intersection point of the inequalities =
`(222.\bar{2}, 583.\bar{3})`

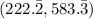
Now, At (0,0) ,

inequality (1), 6×0 + 2×0≤ 2500 ⇒ 0 ≤ 2500 ( true)

Hence, the shaded region of inequality contains the origin.

Similarly, At (0,0), inequality (2) is false,

⇒ The shaded region of inequality (2) does not contain the origin.

Thus, By the above explanation we can plot the shaded region of the system of the given inequalities.