Question

For every dollar increase in the price of music CDs sold by a record label, the demand for the CDs drops by 100. However, 4,000 CDs have already been preordered. If x is the price of a CD, which statement is true about the revenue, R, of the record label?

A.
The equation R = -100x2 + 4,000x can be used to find that the maximum revenue earned by the record label from CD sales is $10,000.
B.
The equation R = -100x2 + 4,000x can be used to find that the maximum revenue earned by the record label from CD sales is $40,000.
C.
The equation R = -4,000x2 + 100x can be used to find that the maximum revenue earned by the record label from CD sales is $10,000.
D.
The equation R = -4,000x2 + 100x can be used to find that the maximum revenue earned by the record label from CD sales is $40,000.

Answer 1

B)

Explanation:

There is a -100x^2 in it because the demand will go down when it increases, and 4000 CDs have been preordered which makes -100x^2+4000x. To find the maximum, first divide by -100. Don't forget to multiply this back! Because we divided by a negative, now we need to find the minimum of x^2-40x. Complete the square to find out the minimum is -400, and multiplying back the -100 you get that the maximum is 40,000 so the answer is B).

Answer 2

Option B

Explanation:

Given that for every dollar increase in the price of music CDs sold by a record label, the demand for the CDs drops by 100. However, 4,000 CDs have already been pre ordered.

x- price of a CD

R-revenue

Since 4000 already ordered for price x, this revenue will not change

= 4000x

dx/dp = -100 (rate of change of x with respect to price is negative 100)

So x= -100p

Revenue = price (x) = -100x^2

So total revenue including for 4000 is

`R = -100x^2 + 4,000x`

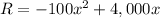
To find maximum we can use derivative test.

-200x+4000 =0 gives x =20

II derivative =-200<0

So maximum revenue when x =20 and max rev

=
`-100(20^2)+4000(20)\\= 40000`

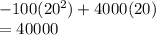
Option B is right