Answer:
As per the statement:
The formula for speed of a tidal wave is:

where
V represents the speed of a tidal wave
g represents the acceleration due to gravity i.e g = 9.8
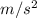 and
and
h represents the depth of the ocean in meters.
It is also given that If the ocean is 500 meters deep.
we have to find the speed of the tidal wave:
h = 500 meter , g = 9.8
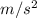
then;
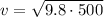

Simplify:
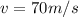
therefore, the speed of a tidal wave will be 70 m/s