Answer:
Option B is correct.
direct variation; k = 5/2
Explanation:
The Direct variation says:
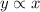
then the equation is of the form:
 ......[1] where k is the constant of variation.
......[1] where k is the constant of variation.
From the given table:
Consider x = -2 and y = -5
Substitute these in [1] to solve for k;
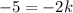
or
5 = 2k
Divide both sides by 2 we get;
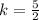
⇒ the equation becomes:
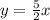
Check:
Take x = 4 and y = 10;
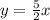
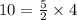
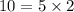
10 = 10 True
Therefore, the direct variation ;
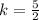 best describe the function represented by the table
best describe the function represented by the table