Answer:
Inverse function are symmetric with respect to line y=x.
It can be written as:
 and
and
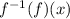
Let's rewrite the given function notation by using y term.
f(x) = 6x-1
i.,e y = 6x-1
Let's solve this equation for x;
Add 1 to both sides we get;
y+1 =6x
Divide both sides by 6 we get;
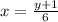
Now, switch the "x" and "y" we have;
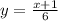
In the function notation:
