Question

. If the radius is doubled and the height is halved what is the ratio of the new volume to the original volume

Answer 1

Answer: Ratio of new volume to original volume is 2:1.

Explanation:

Let the radius of cylinder be 'r'

Let the height of cylinder be 'h'

Original volume of cylinder will be

`V=\pi r^2h`

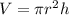
If radius get doubled,

New radius be '2r'

If height get halved,

New height be will be

`(h)/(2)`

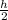
so, Volume of cylinder becomes

`Volume=\pi (2r)^2* (h)/(2)=\pi * 4r^2* (h)/(2)\\\\Volume=2\pi r^2h`

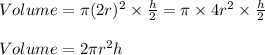
Ratio of new volume to the original volume is given by

`2\pi r^2h:\pi r^2h\\\\2:1`

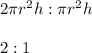
Hence, Ratio of new volume to original volume is 2:1.