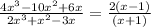Answer:
Cancelling x and (2x-3), we get, the simplest form as
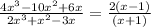
Explanation:
Consider the given two expressions
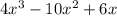 and
and
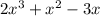 .
.
We solve both expressions seperately,
Consider the first expression
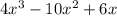
Taking x common from the expression,

The terms in brackets is a quadratic equation, we can solve using middle term splitting method,
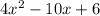
-10x can be written as -4x-6x , we get,
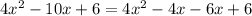
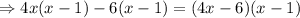
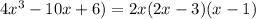
Consider the second term ,
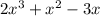
Taking x common from the expression we have,
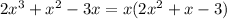
The terms in brackets is a quadratic equation, we can solve using middle term splitting method,
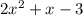
x can be written as 3x-2x
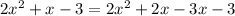
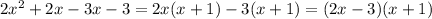
Thus,
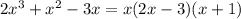
Our expression is
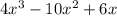 over
over
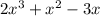
is
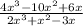
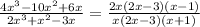
Cancelling same terms from numerator and denominator , thus cancelling x and (2x-3), we get, the simplest form as