Answer:
The expression is given as:
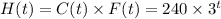 .
.
Explanation:
Sophia expects the number of cows, C, on her farm t years from now to be modeled by the function:
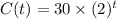
Additionally, she expects the supply of hay, F, in tons, that her crops can provide for each cow t years from now to be modeled by the function

Let H be the total yearly amount of hay produced in Sophia's farm (in tons) t years from now.
Total amount of Hay produced in sophia's farm= Number of cows in farm×Amount of hay required for each cow.
i.e. H(t)=C(t)×F(t)
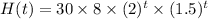
and we know that
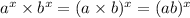
Hence,
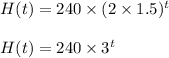 .
.
Hence, the hay produced on Sophia's farm is used exclusively to feed her cows i.e. we need to write the formula of H ( t ) in terms of C(t) and F (t) is:
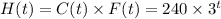 .
.