QUESTION 1
The given equation is
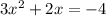
We rewrite in the form,
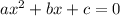
This implies that,
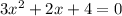
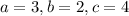
We can use the determinant to find the number of solutions without necessarily solving the equation.


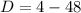
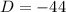
Since the determinant is negative the equation
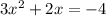
has no solution.
QUESTION 2
The given equation is
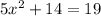
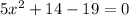
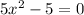
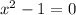

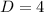
Since the determinant is positive, the equation
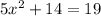
has two solutions.
QUESTION 3
The given equation is
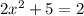
This implies that,
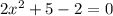
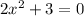
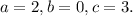
The determinant is


Since the determinant is negative, the equation
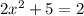
has no solution.
QUESTION 4
The given equation is

We rewrite to obtain,
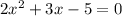
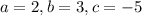
The determinant is
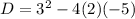
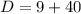

Since the determinant is positive the equation

has two solutions.
QUESTION 5
The given equation is

We rewrite to obtain,
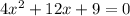
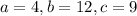
We substitute in the determinant formula to obtain,
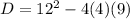
.
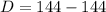
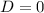
Since the determinant is zero the equation

has only one root.