Question

Solve...........................

Answer 1

Right option is B. x = -3 ± 2√5

Explanation:

Given equation,

x² + 6x - 11 = 0

Using quadratic formula,

`x = \frac{-b ± \sqrt{b^(2) -4ac}}{2a}`

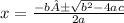
Comparing from general quadratic equation: ax² + bx + c = 0

Here, a= 1 b = 6 and c = -11

so,

`x = \frac{-6 ± \sqrt{6^(2) -4·1·(-11)}}{2·1}`

`x = (-6 ± √(36 +44))/(2)`

`x = (-6 ± √(80))/(2)`

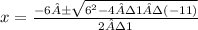
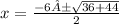
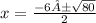
x = -3 ± 2√5

Hence right option is B. x = -3 ± 2√5