Answer: The answer is 35 minutes.
Step-by-step explanation: Given that Gavin goes for a run at a constant pace of 9 minutes per mile and after 10 minutes, Lars started running along the same route, at a constant pace of 7 minutes per mile. We need to find the number of minutes Lars will take to reach Gavin.
In 9 minutes, distance run by Gavin = 1 mile.
So, in 1 minute, distance travelled by Gavin will be
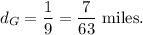
Similarly,
In 7 minutes, distance run by Lars = 1 mile.
So, in 1 minute, distance travelled by Lars will be
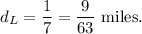
Now, since Lars started after 10 minutes, so distance run by Gavin in those 10 minutes will be
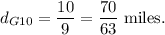
Now, difference between Lars and Gavin's rate of runnings is
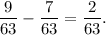
Therefore, the time taken by Lars to reach Gavin is given by
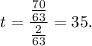
Thus, the required time is 365 minutes.