Question

Which graph is the graph of the following inequality? y ≤ 1/2 (x-6)^2 + 2

Answer 1

ANSWER

The graph in option D

Step-by-step explanation

The given inequality is


`y \leqslant (1)/(2) {(x - 6)}^(2) + 2`

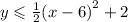
To graph this inequality, we must first of all

graph the corresponding quadratic function.


`y = (1)/(2) {(x - 6)}^(2) + 2`

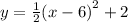
This is a minimum graph with vertex


`(6,2)`

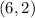
We graph this equation with a solid line.

We then test the inequality using (0,0),


`0 \leqslant (1)/(2) {(0- 6)}^(2) + 2`


`0 \leqslant 20`

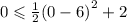
This statement is true so we shade the lower half plane to obtain the graph in option D.