Question

In golf, the lower your score, the better. Negative scores are best of all. Teri scored +1 on each of the first three holes at a nine-hole miniature golf course. Her goal is a total score of -9 or better after she has completed the final six holes.

A. Let h represent the score Teri must average on each of the last six holes in order to meet her goal.Write a two- step inequality you can solve to find h.

b. Solve the inequality

Answer 1

Part a 3(+1) +6h ≤ -9

Part b h ≤ -2

Explanation:

Part a

For the first three holes she scored a +1 on each, 3(+1) = 3 for the first 3 holes

She needs to average h on the last 6 holes, so the total score is 6*h

Her score is

3(+1) +6(h)

It must be -6 or better (better means less than)

3(+1) +6h ≤ -9

Part b

We need to solve this

3 +6h ≤ -9

Subtract three from each side

3-3 +6h ≤ -9-3

6h ≤ -12

Divide each side by 6

6h/6 ≤ -12/6

h ≤ -2

Answer 2

Answer: The answer are given below.

Step-by-step explanation: Given that in golf match, lesser the sores, better is the game. In fact, negative scores are best.

Here given that,

Teri scored +1 on each of the first three holes at a nine-hole miniature golf course and her goal is a total score of -9 or better after she has completed the final six holes.

(A) Given, 'h' represents the score that Teri must average on each of the last six holes in order to meet her goal.

So, if 'x' represents the total score of Teri in the last six holes, then the pair of inequalities are

`3+x\leq -9,\\\\x\leq 6h.`

(B) Solving, we have

`3+x\leq -9\\\\\Rightarrow 3+6h\leq -9\\\\\Rightarrow 6h\leq -12\\\\\Rightarrow h\leq -2.`

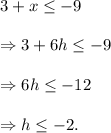
Thus, Teri must score -2 or less in the final six holes to meet her goal.