Answer:
42 pentagons and 18 octagons
Explanation:
We will call the number of pentagons '
 ' and the amount of octagons '
' and the amount of octagons '
 '.
'.
If the sum of both is 60 figures:
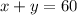
The previous one will be equation 1.
In addition, the problem mentions that there are 354 sides in total, for this we will have to add the amount of sides corresponding to the pentagons: 5x, because the pentagon has 5 sides and we have x pentagons, plus the number of sides corresponding to the octagons: 8y, because the octagon has 8 sides and we have 'y' octagons.
so the equation 2 will be:
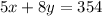
Now we must solve the system of two equations we have.
For this we clear 'x' from equation 1, and substitute in equation 2.
Clearing for 'x' in equation 1:

Substituting in eqution 2:
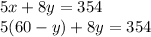
And solving for 'y'
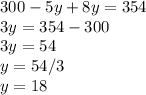
This means there are 18 octagons.
And now to find the number of pentagons, we substitute the value of y = 18 in any of the two equations, i will do it in the equation 1:
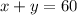
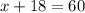
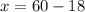

There are 42 pentagons